
Back Binomiaalstelling Afrikaans مبرهنة ذات الحدين Arabic Біном Ньютана Byelorussian Нютонов бином Bulgarian Teorema binomial BJN দ্বিপদী উপপাদ্য Bengali/Bangla Binomna teorema BS کراوەی دوو تێرمی CKB Binomická věta Czech Ньютон биномĕ CV
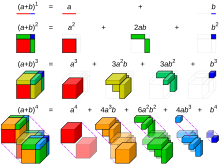
El Binomi de Newton[1][2][3] o teorema del binomi és una fórmula que serveix per a calcular la potència d'un binomi . És per tant una generalització de les fórmules elementals i . Aquestes dues formen part del que s'anomenen Identitats notables, i admeten una demostració gràfica elemental en termes d'àrees de quadrats i rectangles, i volums de cubs i paral·lelepípedes.
La fórmula general utilitza nombres combinatoris, i diu:
on el coeficient binomial és el nombre combinatori definit com a , que es llegeix " sobre ". El conjunt dels coeficients binomials ordenats en fileres amb creixent de dalt a baix constitueixen l'anomenat triangle de Tartaglia, triangle de Pascal o triangle aritmètic.[4]
Exemples:
- per :
- per :
Quan tenim , n'hi ha prou amb escriure-ho com a , amb el que s'obté , i, en general,
.
La fórmula és molt anterior a Newton. La seva història pot trobar-se a l'article Potència d'un Binomi de R. Nolla esmentat més avall com a enllaç extern.
- ↑ Rosa Mateu Martínez, Montserrat Torras i Conangla (Coords.). Diccionari de matemàtiques i estadística. Barcelona: Universitat Politècnica de Catalunya, Enciclopèdia Catalana, 2002. ISBN 8441227926.
- ↑ Råde, Lennart; Westergren, Bertil. Mathematics Handbook for Science and Engineering. Springer. ISBN 978-3-662-08549-3.
- ↑ Bronshtein, I.; Semendiaev, K.. Manual de matemáticas para ingenieros y estudiantes (en castellà). Moscou: MIR, 1977.
- ↑ «binomial theorem | Formula & Definition | Britannica» (en anglès). [Consulta: 12 febrer 2022].

















