Conjectura de Collatz

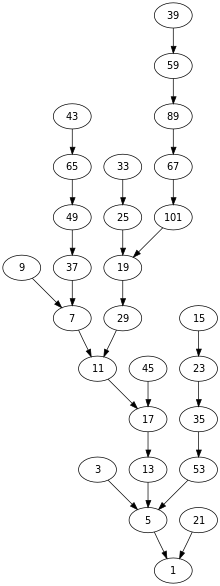
La conjectura de Collatz és un dels problemes no resolts més famosos de les matemàtiques. La conjectura es pregunta si repetir dues operacions aritmètiques simples acabarà transformant cada nombre enter positiu en 1.

Es tracta de seqüències de nombres enters en què cada terme s'obté del terme anterior de la següent manera: si el terme anterior és parell, el terme següent és la meitat del terme anterior. Si el terme anterior és senar, el següent és 3 vegades el terme anterior més 1. La conjectura és que aquestes seqüències sempre arriben a 1, independentment del nombre enter positiu que s'esculli per iniciar la seqüència.

Aquesta conjectura porta el nom del matemàtic Lothar Collatz, que va presentar la idea l'any 1937, dos anys després de doctorar-se.^[1] També es coneix com el problema 3n + 1, la conjectura 3n + 1, la conjectura d'Ulam (per Stanisław Ulam), el problema de Kakutani (per Shizuo Kakutani), la conjectura de Thwaites (per Sir Bryan Thwaites), l'algoritme de Hasse (per Helmut Hasse), o el problema de Syracuse (per la Universitat americana de Syracuse que hi va dedicar molts esforços).^{[Nota 1][2]}

La seqüència de números implicada de vegades es coneix com a seqüència de calamarsa, números de calamarsa o númerals de calamarsa (perquè els valors solen estar subjectes a múltiples baixades i ascensos com la calamarsa en un núvol),^{[Nota 2][3][4]} o com a nombres meravellosos.^[5]

Paul Erdős va dir sobre la conjectura de Collatz: «Les matemàtiques potser no estan preparades per a aquests problemes».^[6] També va oferir 500 US$ per la seva solució.^[7] Jeffrey Lagarias va afirmar el 2010 que la conjectura de Collatz «és un problema extraordinàriament difícil, completament fora de l'abast de les matemàtiques actuals».^[8]

Error de citació: Existeixen etiquetes <ref> pel grup «Nota» però no s'ha trobat l'etiqueta <references group="Nota"/> corresponent.