
Back Aftrek Afrikaans Subtraktion ALS Resta AN طرح Arabic طرح ARZ Resta AST Jakhuqawi Aymara Çıxma Azerbaijani چیخما AZB Алыу Bashkir

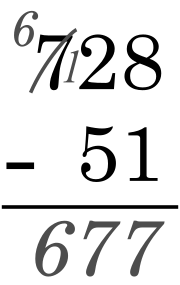

O fewn mathemateg, mae tynnu neu 'tynnu i ffwrdd' yn weithrediad rhifyddol sy'n cynrychioli'r weithrediad o ddileu gwrthrychau o gasgliad, cymryd rhywbeth real neu rif i ffwrdd. Gelwir canlyniad tynnu yn wahaniaeth. Mae tynnu yn cael ei nodi gan y symbol (neu'r nodiant) minws (-). Er enghraifft, yn y llun cyfagos, mae 5 - 2 afal - sy'n golygu 5 afalau gyda 2 yn cael eu cymryd i ffwrdd, yn rhoi cyfanswm o 3 afalau. Felly, y gwahaniaeth rhwng 5 a 2 yw 3, hynny yw, 5 - 2 = 3. Mae tynnu yn cynrychioli tynnu neu ostwng symiau ffisegol a haniaethol gan ddefnyddio gwahanol fathau o wrthrychau, gan gynnwys rhifau negyddol, ffracsiynau, rhifau cymarebol, fectorau, degolion, swyddogaethau a matricsau.
Mae tynnu yn dilyn nifer o batrymau pwysig. Mae'n wrthgymudol (anticommutative), sy'n golygu bod newid y drefn yn newid arwydd yr ateb. Nid yw'n gydgysylltiol, sy'n golygu, pan dynnir mwy na dau rif, mae trefn y rhifau a threfn y weithred yn holl bwysig. Nid yw tynnu 0 yn newid y swm cychwynnol; mae'n rhoi'r un rhif ag oedd yn y grwp (tri afal, minws dim yw tri afal). Mae tynnu hefyd yn dilyn rheolau y gellir eu rhagweld mewn perthynas â gweithrediadau cysylltiedig megis adio a lluosi. Gellir profi'r holl reolau hyn, gan ddechrau gyda thynnu cyfanrifau a chyffredinoli hyd at y rhifau real a thu hwnt. Astudir gweithrediadau deuaidd (binary operations) sy'n parhau â'r patrymau hyn mewn algebra haniaethol.
Tynnu yw un o'r tasgau rhif symlaf. Mae tynnu niferoedd bach iawn o fewn cyrraedd plant ifanc iawn. Mewn addysg gynradd, addysgir disgyblion i dynnu rhifau yn y system ddegol, gan ddechrau gydag digidau unigol cyn mynd i'r afael â phroblemau sy'n gynyddol anos.
Mewn algebra uwch ac mewn algebra cyfrifiadurol, mae mynegiant sy'n cynnwys tynnu e.e. A − B yn cael ei drin fel nodyn llaw-fer ar gyfer adio A + (−B). Felly, mae A − B yn cynnwys dau derm, sef A ac −B.