
Back توزيع ثنائي الحدين Arabic Distribución binómica AST Біномнае размеркаванне Byelorussian দ্বিপদী বন্টন Bengali/Bangla Distribució binomial Catalan Binomické rozdělení Czech Binomialfordelingen Danish Διωνυμική κατανομή Greek Binomial distribution English Distribución binomial Spanish
| Binomialverteilung | |
Wahrscheinlichkeitsfunktion  Drei Wahrscheinlichkeitsfunktionen für Binomialverteilungen mit den Parametern , und
| |
Verteilungsfunktion Drei Verteilungsfunktionen für Binomialverteilungen mit den Parametern , und [Das N in der Legende der drei Verteilungsfunktionen entspricht dem der Dichtefunktionen.] | |
| Parameter | , |
|---|---|
| Träger | |
| Wahrscheinlichkeitsfunktion | |
| Verteilungsfunktion | |
| Erwartungswert | |
| Median | i. A. keine geschlossene Formel, siehe unten |
| Modus | oder |
| Varianz | |
| Schiefe | |
| Wölbung | |
| Entropie | |
| Momenterzeugende Funktion | |
| Charakteristische Funktion | |

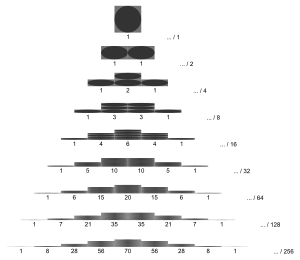
mit und wie im Pascalschen Dreieck
Die Wahrscheinlichkeit, dass eine Kugel in einem Galtonbrett mit acht Ebenen () ins mittlere Fach fällt (), ist .
Die Binomialverteilung ist eine der wichtigsten diskreten Wahrscheinlichkeitsverteilungen.
Sie beschreibt die Anzahl der Erfolge in einer Serie von gleichartigen und unabhängigen Versuchen, die jeweils genau zwei mögliche Ergebnisse haben („Erfolg“ oder „Misserfolg“). Solche Versuchsserien werden auch Bernoulli-Prozesse genannt. Im Urnenmodell wird ein solcher Versuch als Ziehen mit Zurücklegen bezeichnet.
Ist die Erfolgswahrscheinlichkeit bei einem Versuch und die Anzahl der Versuche, dann bezeichnet man mit (auch [1], , [2] oder [3]) die Wahrscheinlichkeit, genau Erfolge zu erzielen (siehe Abschnitt Definition).
Die Binomialverteilung und der Bernoulli-Versuch können mit Hilfe des Galtonbretts veranschaulicht werden. Dabei handelt es sich um eine mechanische Apparatur, in die man Kugeln wirft. Diese fallen dann zufällig in eines von mehreren Fächern, wobei die Aufteilung der Binomialverteilung entspricht. Je nach Konstruktion sind unterschiedliche Parameter und möglich.
Obwohl die Binomialverteilung bereits lange vorher bekannt war, wurde der Begriff zum ersten Mal 1911 in einem Buch von George Udny Yule verwendet.[4]
- ↑ Binomialverteilung. In: P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 39.
- ↑ Peter Kissel: MAC08 Stochastik (Teil 2). Studiengemeinschaft Darmstadt 2014, S. 12.
- ↑ Bigalke, Köhler: Mathematik 13.2 Grund- und Leistungskurs. Cornelsen, Berlin 2000, S. 130.
- ↑ George Udny Yule: An Introduction to the Theory of Statistics. Griffin, London 1911, S. 287.





![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)


























