Paraboloid

Ein Paraboloid ist eine Fläche zweiter Ordnung (Quadrik) und wird in den einfachsten Fällen durch eine Gleichung beschrieben:

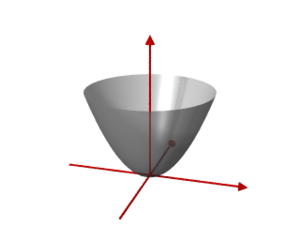
• ${\displaystyle P1\colon \ z=x^{2}+y^{2}}$ für elliptisches Paraboloid
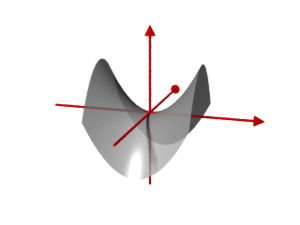
• ${\displaystyle P2\colon \ z=x^{2}-y^{2}}$ für ein hyperbolisches Paraboloid

Elliptische Paraboloide begegnen einem beispielsweise als Oberflächen von Satellitenschüsseln und als Energieentwertungsdiagramme^[1] beim Stoß rauer Starrkörper.
Hyperbolische Paraboloide sind Sattelflächen. Sie enthalten Geraden und werden deswegen von Architekten und Bauingenieuren als leicht modellierbare Dachformen (hyperbolische Paraboloidschalen) verwendet^[2].

Anhand der Gleichungen erkennt man, dass beide Flächen viele Parabeln enthalten, was zur Namensgebung beigetragen hat:

${\displaystyle P1}$ ist eine Rotationsfläche. ${\displaystyle P1}$ entsteht durch Rotation der Parabel in der x-z-Ebene mit der Gleichung ${\displaystyle z=x^{2}}$ um die z-Achse.
${\displaystyle P2}$ ist keine Rotationsfläche. Aber auch bei ${\displaystyle P2}$ ist bis auf zwei Ausnahmen jeder Schnitt mit einer Ebene durch die z-Achse eine Parabel. Z. B. ist der Schnitt mit der Ebene ${\displaystyle x=0}$ (y-z-Ebene) die Parabel ${\displaystyle z=-y^{2}}$.
Beide Flächen lassen sich als Schiebflächen auffassen und lassen sich durch verschieben einer Parabel entlang einer zweiten Parabel erzeugen.

Allerdings gibt es auch wesentliche Unterschiede:

• ${\displaystyle P1}$ besitzt als Höhenschnitte Kreise (für konstantes ${\displaystyle z}$). Im allgemeinen Fall sind es Ellipsen (siehe unten), was sich im Namenszusatz widerspiegelt,
• ${\displaystyle P2}$ besitzt als Höhenschnitte Hyperbeln oder Geraden (für ${\displaystyle z=0}$), was den Zusatz hyperbolisch rechtfertigt.

Ein hyperbolisches Paraboloid ist nicht mit einem Hyperboloid zu verwechseln.

1. ↑ K.-E. Kurrer: Zur Darstellung der Energietransformation beim ebenen gekoppelten Reibungsstoß mit Hilfe des Energieentwertungsdiagramms. In: Cassius Alexandru, Günter Gödert, Uwe Görn, Roland Parchem und Joachim Villwock (Hrsg.): Beiträge zur Mechanik. Festschrift zum 65. Geburtstag von Prof. Dr. Rudolf Trostel. Universitätsbibliothek der TU Berlin, Abt. Publikation, Berlin 1993, ISBN 3-7983-1581-7, S. 148–169.
2. ↑ K.-E. Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin 2018, S. 743–747, ISBN 978-3-433-03229-9