
Back Funció d'Anger Catalan Anger-függvény Hungarian Funzioni di Anger Italian Функция Ангера Russian Ангерова функција Serbian Angers funktion Swedish 安格尔函数 Chinese
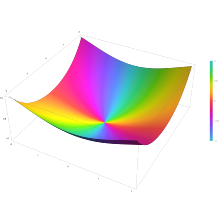
In mathematics, the Anger function, introduced by C. T. Anger (1855), is a function defined as
with complex parameter and complex variable .[1] It is closely related to the Bessel functions.
The Weber function (also known as Lommel–Weber function), introduced by H. F. Weber (1879), is a closely related function defined by
and is closely related to Bessel functions of the second kind.
- ^ Prudnikov, A.P. (2001) [1994], "Anger function", Encyclopedia of Mathematics, EMS Press



