
Back كرة بلوخ Arabic Esfera de Bloch Catalan Bloch-Kugel German Σφαίρα Μπλοχ Greek Esfera de Bloch Spanish کره بلوخ Persian Sphère de Bloch French ספירת בלוך HE Sfera di Bloch Italian ブロッホ球 Japanese
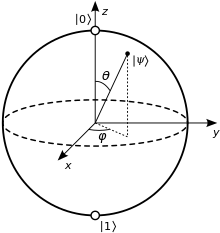
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.[1]
Mathematically each quantum mechanical system is associated with a separable complex Hilbert space . A pure state of a quantum system is represented by a non-zero vector in . As the vectors and (with ) represent the same state, the level of the quantum system corresponds to the dimension of the Hilbert space and pure states can be represented as equivalence classes, or, rays in a projective Hilbert space .[2] For a two-dimensional Hilbert space, the space of all such states is the complex projective line This is the Bloch sphere, which can be mapped to the Riemann sphere.
The Bloch sphere is a unit 2-sphere, with antipodal points corresponding to a pair of mutually orthogonal state vectors. The north and south poles of the Bloch sphere are typically chosen to correspond to the standard basis vectors and , respectively, which in turn might correspond e.g. to the spin-up and spin-down states of an electron. This choice is arbitrary, however. The points on the surface of the sphere correspond to the pure states of the system, whereas the interior points correspond to the mixed states.[3][4] The Bloch sphere may be generalized to an n-level quantum system, but then the visualization is less useful.
The natural metric on the Bloch sphere is the Fubini–Study metric. The mapping from the unit 3-sphere in the two-dimensional state space to the Bloch sphere is the Hopf fibration, with each ray of spinors mapping to one point on the Bloch sphere.
- ^ Bloch 1946.
- ^ Bäuerle & de Kerf 1990, pp. 330, 341.
- ^ Nielsen & Chuang 2000.
- ^ "Bloch sphere | Quantiki".








