
Back دالة بول Arabic Булева функцыя Byelorussian Funció booleana Catalan Boolesche Funktion German Función booleana Spanish Funtzio boolear Basque تابع بولی Persian Fonction booléenne French Función booleana Galician बूलीय फलन Hindi
| Logical connectives | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||
| Related concepts | ||||||||||||||||||||||||||
| Applications | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually {true, false}, {0,1} or {-1,1}).[1][2] Alternative names are switching function, used especially in older computer science literature,[3][4] and truth function (or logical function), used in logic. Boolean functions are the subject of Boolean algebra and switching theory.[5]
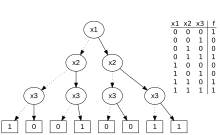
A Boolean function takes the form , where is known as the Boolean domain and is a non-negative integer called the arity of the function. In the case where , the function is a constant element of . A Boolean function with multiple outputs, with is a vectorial or vector-valued Boolean function (an S-box in symmetric cryptography).[6]
There are different Boolean functions with arguments; equal to the number of different truth tables with entries.
Every -ary Boolean function can be expressed as a propositional formula in variables , and two propositional formulas are logically equivalent if and only if they express the same Boolean function.
- ^ "Boolean function - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-05-03.
- ^ Weisstein, Eric W. "Boolean Function". mathworld.wolfram.com. Retrieved 2021-05-03.
- ^ "switching function". TheFreeDictionary.com. Retrieved 2021-05-03.
- ^ Davies, D. W. (December 1957). "Switching Functions of Three Variables". IRE Transactions on Electronic Computers. EC-6 (4): 265–275. doi:10.1109/TEC.1957.5222038. ISSN 0367-9950.
- ^ McCluskey, Edward J. (2003-01-01), "Switching theory", Encyclopedia of Computer Science, GBR: John Wiley and Sons Ltd., pp. 1727–1731, ISBN 978-0-470-86412-8, retrieved 2021-05-03
- ^ Cite error: The named reference
:2was invoked but never defined (see the help page).





















