Cantor distribution

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Cantor distribution" – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message)

Cantor

Cumulative distribution function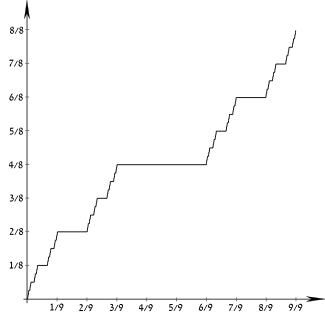
Parameters	none
Support	Cantor set, a subset of [0,1]
PMF	none
CDF	Cantor function
Mean	1/2
Median	anywhere in [1/3, 2/3]
Mode	n/a
Variance	1/8
Skewness	0
Excess kurtosis	−8/5
MGF	${\displaystyle e^{t/2}\prod _{k=1}^{\infty }\cosh \left({\frac {t}{3^{k}}}\right)}$
CF	${\displaystyle e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\right)}$

The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function.

This distribution has neither a probability density function nor a probability mass function, since although its cumulative distribution function is a continuous function, the distribution is not absolutely continuous with respect to Lebesgue measure, nor does it have any point-masses. It is thus neither a discrete nor an absolutely continuous probability distribution, nor is it a mixture of these. Rather it is an example of a singular distribution.

Its cumulative distribution function is continuous everywhere but horizontal almost everywhere, so is sometimes referred to as the Devil's staircase, although that term has a more general meaning.