
Back اتحاد مركزي Arabic Soustřednost Czech Konzentrizität German Concéntrico Spanish Kontsentrilised objektid Estonian هممرکز Persian Concentricité French עצמים קונצנטריים HE संकेन्द्रीय वृत्त Hindi Konsentris ID
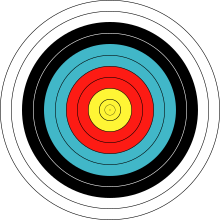

In geometry, two or more objects are said to be concentric when they share the same center. Any pair of (possibly unalike) objects with well-defined centers can be concentric, including circles, spheres, regular polygons, regular polyhedra, parallelograms, cones, conic sections, and quadrics.[1]
Geometric objects are coaxial if they share the same axis (line of symmetry). Geometric objects with a well-defined axis include circles (any line through the center), spheres, cylinders,[2] conic sections, and surfaces of revolution.
Concentric objects are often part of the broad category of whorled patterns, which also includes spirals (a curve which emanates from a point, moving farther away as it revolves around the point).
- ^
Circles: Alexander, Daniel C.; Koeberlein, Geralyn M. (2009), Elementary Geometry for College Students, Cengage Learning, p. 279, ISBN 9781111788599
Spheres: Apostol (2013)
Regular polygons: Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, The University Press, p. 107
Regular polyhedra: Gillard, Robert D. (1987), Comprehensive Coordination Chemistry: Theory & background, Pergamon Press, pp. 137, 139, ISBN 9780080262321.
- ^ Spurk, Joseph; Aksel, Nuri (2008), Fluid Mechanics, Springer, p. 174, ISBN 9783540735366.