
Back Behoud van massa Afrikaans قانون حفظ الكتلة Arabic Llei de caltenimientu de la materia AST Закон захавання масы Byelorussian Закон за запазване на масата Bulgarian Zakon održanja mase BS Llei de conservació de la massa Catalan بمێنیی بارستە CKB Zákon zachování hmotnosti Czech Масса сыхланнин саккунĕ CV
This article needs additional citations for verification. (May 2020) |
| Part of a series on |
| Continuum mechanics |
|---|
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter the mass of the system must remain constant over time.[1]
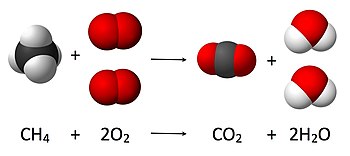
The law implies that mass can neither be created nor destroyed, although it may be rearranged in space, or the entities associated with it may be changed in form. For example, in chemical reactions, the mass of the chemical components before the reaction is equal to the mass of the components after the reaction. Thus, during any chemical reaction and low-energy thermodynamic processes in an isolated system, the total mass of the reactants, or starting materials, must be equal to the mass of the products.
The concept of mass conservation is widely used in many fields such as chemistry, mechanics, and fluid dynamics. Historically, mass conservation in chemical reactions was primarily demonstrated in the 17th century[2] and finally confirmed by Antoine Lavoisier in the late 18th century. The formulation of this law was of crucial importance in the progress from alchemy to the modern natural science of chemistry.
In reality, the conservation of mass only holds approximately and is considered part of a series of assumptions in classical mechanics. The law has to be modified to comply with the laws of quantum mechanics and special relativity under the principle of mass–energy equivalence, which states that energy and mass form one conserved quantity. For very energetic systems the conservation of mass only is shown not to hold, as is the case in nuclear reactions and particle-antiparticle annihilation in particle physics.
Mass is also not generally conserved in open systems. Such is the case when any energy or matter is allowed into, or out of, the system. However, unless radioactivity or nuclear reactions are involved, the amount of energy entering or escaping such systems (as heat, mechanical work, or electromagnetic radiation) is usually too small to be measured as a change in the mass of the system.
For systems that include large gravitational fields, general relativity has to be taken into account; thus mass–energy conservation becomes a more complex concept, subject to different definitions, and neither mass nor energy is as strictly and simply conserved as is the case in special relativity.
- ^ John Olmsted; Gregory M. Williams (1997). Chemistry: The Molecular Science (illustrated ed.). Jones & Bartlett Learning. p. 69. ISBN 978-0-8151-8450-8. Extract of page 69
- ^ Lavoisier's Method
