Dijkstra's algorithm

Dijkstra's algorithm

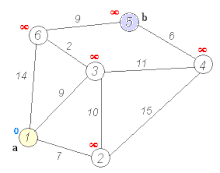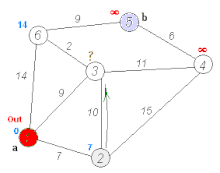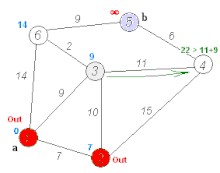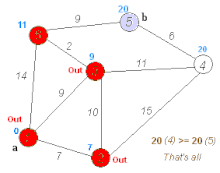Dijkstra's algorithm to find the shortest path between a and b. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors.
Class	Search algorithm Greedy algorithm Dynamic programming[1]
Data structure	Graph Usually used with priority queue or heap for optimization[2][3]
Worst-case performance	${\displaystyle \Theta (|E|+|V|\log |V|)}$[3]

Dijkstra's algorithm (/ˈdaɪkstrəz/ DYKE-strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.^[4][5][6]

Dijkstra's algorithm finds the shortest path from a given source node to every other node.^{[7]: 196–206} It can be used to find the shortest path to a specific destination node, by terminating the algorithm after determining the shortest path to the destination node. For example, if the nodes of the graph represent cities, and the costs of edges represent the average distances between pairs of cities connected by a direct road, then Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. A common application of shortest path algorithms is network routing protocols, most notably IS-IS (Intermediate System to Intermediate System) and OSPF (Open Shortest Path First). It is also employed as a subroutine in algorithms such as Johnson's algorithm.

The algorithm uses a min-priority queue data structure for selecting the shortest paths known so far. Before more advanced priority queue structures were discovered, Dijkstra's original algorithm ran in ${\displaystyle \Theta (|V|^{2})}$ time, where ${\displaystyle |V|}$ is the number of nodes.^[8][9] Fredman & Tarjan 1984 proposed a Fibonacci heap priority queue to optimize the running time complexity to ${\displaystyle \Theta (|E|+|V|\log |V|)}$. This is asymptotically the fastest known single-source shortest-path algorithm for arbitrary directed graphs with unbounded non-negative weights. However, specialized cases (such as bounded/integer weights, directed acyclic graphs etc.) can be improved further. If preprocessing is allowed, algorithms such as contraction hierarchies can be up to seven orders of magnitude faster.

Dijkstra's algorithm is commonly used on graphs where the edge weights are positive integers or real numbers. It can be generalized to any graph where the edge weights are partially ordered, provided the subsequent labels (a subsequent label is produced when traversing an edge) are monotonically non-decreasing.^[10][11]

In many fields, particularly artificial intelligence, Dijkstra's algorithm or a variant offers a uniform cost search and is formulated as an instance of the more general idea of best-first search.^[12]