Back نظرية النظم التحريكية Arabic Teoria de sistemes dinàmics Catalan Dynamisches System (Systemtheorie) German تئوری سامانههای پویا Persian Dynaaminen systeemiteoria Finnish Théorie des systèmes dynamiques French Teori sistem dinamik ID Analisi dei sistemi dinamici Italian Teoria układów dynamicznych Polish Dynamical systems theory SIMPLE
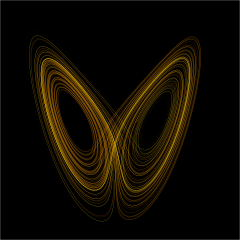
Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.
This theory deals with the long-term qualitative behavior of dynamical systems, and studies the nature of, and when possible the solutions of, the equations of motion of systems that are often primarily mechanical or otherwise physical in nature, such as planetary orbits and the behaviour of electronic circuits, as well as systems that arise in biology, economics, and elsewhere. Much of modern research is focused on the study of chaotic systems and bizarre systems.
This field of study is also called just dynamical systems, mathematical dynamical systems theory or the mathematical theory of dynamical systems.