Back بعد كسيري Arabic Фрактална размерност Bulgarian Fraktalna dimenzija BS Dimensió fractal Catalan Fraktale Dimension German Μορφοκλασματική διάσταση Greek Dimensión fractal Spanish بعد برخالی Persian Dimension fractale French Fraktalna dimenzija Croatian
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.[1][2][3]
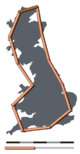
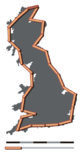
The main idea of "fractured" dimensions has a long history in mathematics, but the term itself was brought to the fore by Benoit Mandelbrot based on his 1967 paper on self-similarity in which he discussed fractional dimensions.[4] In that paper, Mandelbrot cited previous work by Lewis Fry Richardson describing the counter-intuitive notion that a coastline's measured length changes with the length of the measuring stick used (see Fig. 1). In terms of that notion, the fractal dimension of a coastline quantifies how the number of scaled measuring sticks required to measure the coastline changes with the scale applied to the stick.[5] There are several formal mathematical definitions of fractal dimension that build on this basic concept of change in detail with change in scale: see the section Examples.
Ultimately, the term fractal dimension became the phrase with which Mandelbrot himself became most comfortable with respect to encapsulating the meaning of the word fractal, a term he created. After several iterations over years, Mandelbrot settled on this use of the language: "...to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants."[6]
One non-trivial example is the fractal dimension of a Koch snowflake. It has a topological dimension of 1, but it is by no means rectifiable: the length of the curve between any two points on the Koch snowflake is infinite. No small piece of it is line-like, but rather it is composed of an infinite number of segments joined at different angles. The fractal dimension of a curve can be explained intuitively by thinking of a fractal line as an object too detailed to be one-dimensional, but too simple to be two-dimensional.[7] Therefore, its dimension might best be described not by its usual topological dimension of 1 but by its fractal dimension, which is often a number between one and two; in the case of the Koch snowflake, it is approximately 1.2619.
- ^ Cite error: The named reference
Falconerwas invoked but never defined (see the help page). - ^ Cite error: The named reference
space fillingwas invoked but never defined (see the help page). - ^ Vicsek, Tamás (1992). Fractal growth phenomena. World Scientific. p. 10. ISBN 978-981-02-0668-0.
- ^ Mandelbrot, B. (1967). "How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension". Science. 156 (3775): 636–8. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158. S2CID 15662830. Archived from the original on 2021-10-19. Retrieved 2020-11-12.
- ^ Cite error: The named reference
Mandelbrot1983was invoked but never defined (see the help page). - ^ Edgar, Gerald (2007). Measure, Topology, and Fractal Geometry. Springer. p. 7. ISBN 978-0-387-74749-1.
- ^ Harte, David (2001). Multifractals. Chapman & Hall. pp. 3–4. ISBN 978-1-58488-154-4.