
Back تشاكل الزمر Arabic Qrupların homomorfizmi Azerbaijani Homomorfisme de grups Catalan Grupový homomorfismus Czech Gruppehomomorfi Danish Gruppenhomomorphismus German Grupa homomorfio Esperanto Homomorfismo de grupos Spanish همریختی گروهی Persian Ryhmähomomorfismi Finnish
| Algebraic structure → Group theory Group theory |
|---|
 |
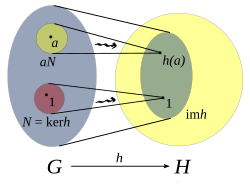
In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that
where the group operation on the left side of the equation is that of G and on the right side that of H.
From this property, one can deduce that h maps the identity element eG of G to the identity element eH of H,
and it also maps inverses to inverses in the sense that
Hence one can say that h "is compatible with the group structure".
In areas of mathematics where one considers groups endowed with additional structure, a homomorphism sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of topological groups is often required to be continuous.



