Back Teorema de la bola peluda AST Teorema de la bola peluda Catalan Sætningen om den behårede kugle Danish Satz vom Igel German Teoremo pri erinaco Esperanto Teorema de la bola peluda Spanish قضیه توپ مودار Persian Karvapallolause Finnish Théorème de la boule chevelue French משפט הכדור השעיר HE

Hairy ball theorem

A failed attempt to comb a hairy 3-ball (2-sphere), leaving a tuft at each pole
A hairy doughnut (2-torus), on the other hand, is quite easily combable.
A continuous tangent vector field on a 2-sphere with only one pole, in this case a dipole field with index 2. See also an animated version of this graphic.
A hair whorl

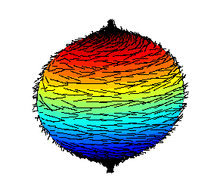
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe)[1] states that there is no nonvanishing continuous tangent vector field on even-dimensional n-spheres.[2][3] For the ordinary sphere, or 2‑sphere, if f is a continuous function that assigns a vector in ℝ3 to every point p on a sphere such that f(p) is always tangent to the sphere at p, then there is at least one pole, a point where the field vanishes (a p such that f(p) = 0).

The theorem was first proved by Henri Poincaré for the 2-sphere in 1885,[4] and extended to higher even dimensions in 1912 by Luitzen Egbertus Jan Brouwer.[5]

The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut".[6]

  1. ^ Renteln, Paul (2013). Manifolds, Tensors, and Forms: An Introduction for Mathematicians and Physicists. Cambridge Univ. Press. p. 253. ISBN 978-1107659698.
  2. ^ Burns, Keith; Gidea, Marian (2005). Differential Geometry and Topology: With a View to Dynamical Systems. CRC Press. p. 77. ISBN 1584882530.
  3. ^ Schwartz, Richard Evan (2011). Mostly Surfaces. American Mathematical Society. pp. 113–114. ISBN 978-0821853689.
  4. ^ Poincaré, H. (1885), "Sur les courbes définies par les équations différentielles", Journal de Mathématiques Pures et Appliquées, 4: 167–244
  5. ^ Georg-August-Universität Göttingen Archived 2006-05-26 at the Wayback Machine - L.E.J. Brouwer. Über Abbildung von Mannigfaltigkeiten / Mathematische Annalen (1912) Volume: 71, page 97-115; ISSN: 0025-5831; 1432-1807/e, full text
  6. ^ Richeson, David S. (23 July 2019). Euler's gem : the polyhedron formula and the birth of topology (New Princeton science library ed.). Princeton. p. 5. ISBN 978-0691191997.{{cite book}}: CS1 maint: location missing publisher (link)
From Wikipedia, the free encyclopedia · View on Wikipedia

Developed by Nelliwinne