
Back Estimació de la densitat del nucli Catalan Kerndichteschätzer German Estimación de Densidad de Kernel Spanish Ydinestimointi Finnish Estimation par noyau French Stima kernel di densità Italian カーネル密度推定 Japanese 커널 밀도 추정 Korean Estymator jądrowy gęstości Polish Estimativa de densidade kernel Portuguese
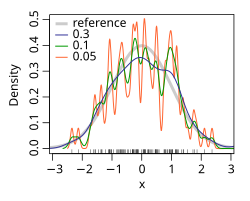
In statistics, kernel density estimation (KDE) is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function of a random variable based on kernels as weights. KDE answers a fundamental data smoothing problem where inferences about the population are made based on a finite data sample. In some fields such as signal processing and econometrics it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form.[1][2] One of the famous applications of kernel density estimation is in estimating the class-conditional marginal densities of data when using a naive Bayes classifier, which can improve its prediction accuracy.[3]
- ^ Rosenblatt, M. (1956). "Remarks on Some Nonparametric Estimates of a Density Function". The Annals of Mathematical Statistics. 27 (3): 832–837. doi:10.1214/aoms/1177728190.
- ^ Parzen, E. (1962). "On Estimation of a Probability Density Function and Mode". The Annals of Mathematical Statistics. 33 (3): 1065–1076. doi:10.1214/aoms/1177704472. JSTOR 2237880.
- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome H. (2001). The Elements of Statistical Learning : Data Mining, Inference, and Prediction : with 200 full-color illustrations. New York: Springer. ISBN 0-387-95284-5. OCLC 46809224.