
Back Baumkalkül German Árbol semántico Spanish Méthode des tableaux French タブローの方法 Japanese Semantisch tableau Dutch Tableau (system dowodzenia twierdzeń) Polish Método dos Tableaux Analíticos Portuguese
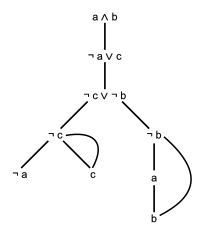
In proof theory, the semantic tableau[1] (/tæˈbloʊ, ˈtæbloʊ/; plural: tableaux), also called an analytic tableau,[2] truth tree,[1] or simply tree,[2] is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic.[1] An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula.[3] The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.[4]
A method of truth trees contains a fixed set of rules for producing trees from a given logical formula, or set of logical formulas. Those trees will have more formulas at each branch, and in some cases, a branch can come to contain both a formula and its negation, which is to say, a contradiction. In that case, the branch is said to close.[1] If every branch in a tree closes, the tree itself is said to close. In virtue of the rules for construction of tableaux, a closed tree is a proof that the original formula, or set of formulas, used to construct it was itself self-contradictory,[1] and therefore false. Conversely, a tableau can also prove that a logical formula is tautologous: if a formula is tautologous, its negation is a contradiction, so a tableau built from its negation will close.[1]
- ^ a b c d e f Howson, Colin (1997). Logic with trees: an introduction to symbolic logic. London; New York: Routledge. pp. ix, x, 24–29, 47. ISBN 978-0-415-13342-5.
- ^ a b Restall, Greg (2006). Logic: an introduction. Fundamentals of philosophy. London; New York: Routledge. pp. 5, 42, 55. ISBN 978-0-415-40067-1. OCLC 63115330.
- ^ Howson 2005, p. 27.
- ^ Girle 2014.