
Back نموذج غلافي للنواة Arabic نموونەی چینی ناوکی CKB Schalenmodell (Kernphysik) German Modelo de capas nuclear Spanish مدل پوستهای هسته Persian Modèle en couches French Héjmodell Hungarian Model kulit nuklir ID Modello nucleare a shell Italian 殻模型 Japanese
| Nuclear physics |
|---|
 |
In nuclear physics, atomic physics, and nuclear chemistry, the nuclear shell model utilizes the Pauli exclusion principle to model the structure of atomic nuclei in terms of energy levels.[1] The first shell model was proposed by Dmitri Ivanenko (together with E. Gapon) in 1932. The model was developed in 1949 following independent work by several physicists, most notably Maria Goeppert Mayer and J. Hans D. Jensen, who received the 1963 Nobel Prize in Physics for their contributions to this model, and Eugene Wigner, who received the Nobel Prize alongside them for his earlier groundlaying work on the atomic nuclei.[2]
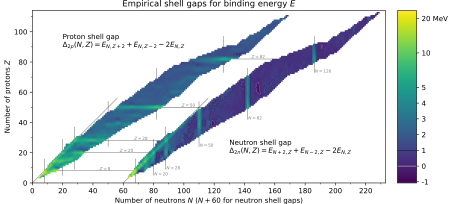
The nuclear shell model is partly analogous to the atomic shell model, which describes the arrangement of electrons in an atom, in that a filled shell results in better stability. When adding nucleons (protons and neutrons) to a nucleus, there are certain points where the binding energy of the next nucleon is significantly less than the last one. This observation that there are specific magic quantum numbers of nucleons (2, 8, 20, 28, 50, 82, and 126) that are more tightly bound than the following higher number is the origin of the shell model.
The shells for protons and neutrons are independent of each other. Therefore, there can exist both "magic nuclei", in which one nucleon type or the other is at a magic number, and "doubly magic quantum nuclei", where both are. Due to variations in orbital filling, the upper magic numbers are 126 and, speculatively, 184 for neutrons, but only 114 for protons, playing a role in the search for the so-called island of stability. Some semi-magic numbers have been found, notably Z = 40, which gives the nuclear shell filling for the various elements; 16 may also be a magic number.[3]
To get these numbers, the nuclear shell model starts with an average potential with a shape somewhere between the square well and the harmonic oscillator. To this potential, a spin-orbit term is added. Even so, the total perturbation does not coincide with the experiment, and an empirical spin-orbit coupling must be added with at least two or three different values of its coupling constant, depending on the nuclei being studied.
The magic numbers of nuclei, as well as other properties, can be arrived at by approximating the model with a three-dimensional harmonic oscillator plus a spin–orbit interaction. A more realistic but complicated potential is known as the Woods–Saxon potential.
- ^ "Shell Model of Nucleus". HyperPhysics.
- ^ Nobel Lectures, Physics 1963-1970. Amsterdam, Netherlands: Elsevier Publishing Company. 1972. Retrieved May 19, 2023.
- ^ Ozawa, A.; Kobayashi, T.; Suzuki, T.; Yoshida, K.; Tanihata, I. (2000). "New Magic Number, N=16, near the Neutron Drip Line". Physical Review Letters. 84 (24): 5493–5. Bibcode:2000PhRvL..84.5493O. doi:10.1103/PhysRevLett.84.5493. PMID 10990977. (this refers to the nuclear drip line)
- ^ Wang, Meng; Audi, G.; Kondev, F. G.; Huang, W.J.; Naimi, S.; Xu, Xing (March 2017). "The AME2016 atomic mass evaluation (II). Tables, graphs and references". Chinese Physics C. 41 (3): 030003. Bibcode:2017ChPhC..41c0003W. doi:10.1088/1674-1137/41/3/030003. hdl:11858/00-001M-0000-0010-23E8-5. ISSN 1674-1137.
