
Back Ordnungsstatistik German Estadísticos de orden Spanish آماره ترتیبی Persian Statistique d'ordre French סטטיסטי הסדר HE Statistica d'ordine Italian 順序統計量 Japanese 순서통계량 Korean Geordende steekproef Dutch Statystyka pozycyjna Polish
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (December 2010) |
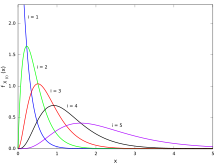
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value.[1] Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.
Important special cases of the order statistics are the minimum and maximum value of a sample, and (with some qualifications discussed below) the sample median and other sample quantiles.
When using probability theory to analyze order statistics of random samples from a continuous distribution, the cumulative distribution function is used to reduce the analysis to the case of order statistics of the uniform distribution.
- ^ David, H. A.; Nagaraja, H. N. (2003). Order Statistics. Wiley Series in Probability and Statistics. doi:10.1002/0471722162. ISBN 9780471722168.