
Back سير عشوائي Arabic Случайно обхождане Bulgarian Camí aleatori Catalan Náhodná procházka Czech Random walk Danish Irrfahrt (Stochastik) German Hazarda promenado Esperanto Camino aleatorio Spanish ولگشت Persian Satunnaiskulku Finnish
| Part of a series on statistics |
| Probability theory |
|---|
 |
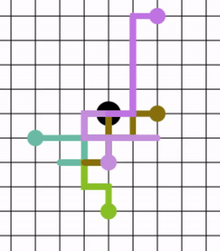
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term random walk was first introduced by Karl Pearson in 1905.[1]
Realizations of random walks can be obtained by Monte Carlo simulation.[2]
- ^ Pearson, Karl (1905). "The Problem of the Random Walk". Nature. 72 (1865): 294. Bibcode:1905Natur..72..294P. doi:10.1038/072294b0. S2CID 4010776.
- ^ Theory and Applications of Monte Carlo Simulations. (2013). Kroatien: IntechOpen. Page 229, https://books.google.com/books?id=3HWfDwAAQBAJ&pg=PA229
