
Back Àtom de Rydberg Catalan Rydberg-Zustand German Átomo de Rydberg Spanish اتم ریدبرگ Persian Atome de Rydberg French Atomo di Rydberg Italian Rydbergatom NB Atomy rydbergowskie Polish Ридберговские атомы Russian Rydberg atomu Turkish

A Rydberg atom is an excited atom with one or more electrons that have a very high principal quantum number, n.[1][2] The higher the value of n, the farther the electron is from the nucleus, on average. Rydberg atoms have a number of peculiar properties including an exaggerated response to electric and magnetic fields,[3] long decay periods and electron wavefunctions that approximate, under some conditions, classical orbits of electrons about the nuclei.[4] The core electrons shield the outer electron from the electric field of the nucleus such that, from a distance, the electric potential looks identical to that experienced by the electron in a hydrogen atom.[5]
In spite of its shortcomings, the Bohr model of the atom is useful in explaining these properties. Classically, an electron in a circular orbit of radius r, about a hydrogen nucleus of charge +e, obeys Newton's second law:
where k = 1/(4πε0).
Orbital momentum is quantized in units of ħ:
- .
Combining these two equations leads to Bohr's expression for the orbital radius in terms of the principal quantum number, n:
It is now apparent why Rydberg atoms have such peculiar properties: the radius of the orbit scales as n2 (the n = 137 state of hydrogen has an atomic radius ~1 μm) and the geometric cross-section as n4. Thus, Rydberg atoms are extremely large, with loosely bound valence electrons, easily perturbed or ionized by collisions or external fields.
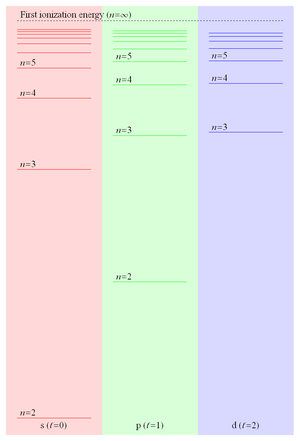
Because the binding energy of a Rydberg electron is proportional to 1/r and hence falls off like 1/n2, the energy level spacing falls off like 1/n3 leading to ever more closely spaced levels converging on the first ionization energy. These closely spaced Rydberg states form what is commonly referred to as the Rydberg series. Figure 2 shows some of the energy levels of the lowest three values of orbital angular momentum in lithium.
- ^ Gallagher, Thomas F. (1994). Rydberg Atoms. Cambridge University Press. ISBN 978-0-521-02166-1.
- ^ Šibalić, Nikola; S Adams, Charles (2018). Rydberg Physics. IOP Publishing. Bibcode:2018ryph.book.....S. doi:10.1088/978-0-7503-1635-4. ISBN 9780750316354.
- ^ Metcalf Research Group (2004-11-08). "Rydberg Atom Optics". Stony Brook University. Archived from the original on August 26, 2005. Retrieved 2008-07-30.
- ^ J. Murray-Krezan (2008). "The classical dynamics of Rydberg Stark atoms in momentum space". American Journal of Physics. 76 (11): 1007–1011. Bibcode:2008AmJPh..76.1007M. doi:10.1119/1.2961081.
- ^ Nolan, James (2005-05-31). "Rydberg Atoms and the Quantum Defect". Davidson College. Archived from the original on 2015-12-06. Retrieved 2008-07-30.


