Situo de verticoj

En geometrio, situo de verticoj estas aro de punktoj en spaco priskribita per iliaj relativaj pozicioj, ĉe kiu la punktoj estas verticoj de hiperpluredro (plurlatero, pluredro, plurĉelo, ...) aŭ kahelaro.

Ekzemple situo de verticoj de kvadrato estas kvar punktoj A, B, C, D en ebeno, tiaj ke la distancoj estas interegalaj AB=BC=CD=DA kaj la anguloj estas ∟ABC=∟BCD=∟CDA=∟DAB=90°.

Verticoj en la sama situo povas esti koneksaj per lateroj en malsamaj manieroj. Ekzemple la kvinlatero kaj stelokvinlatero havas la saman situon de verticoj, dum la (sekundo, dua) trakonektas alternaj verticoj.

Kvinlatero	Stelokvinlatero
Du malsamaj plurlateroj kun la sama situo de verticoj

Tio ke du hiperpluredroj havas la saman situon de verticoj alivorte povas esti skribite kiel ke ili havas la saman 0-skeleton.

Situo de verticoj estas ofte priskribita per la konveksa koverto, kiu mem estas hiperpluredro kiu enhavas la fontan hiperpluredron. Ekzemple, konveksa koverto de la regula stelokvinlatero estas la regula kvinlatero. Tamen, ĉi tiu maniero ne ĉiam taŭgas. Ekzemple, konveksa koverto de nekonveksa kvarlatero povas esti triangulo, kaj la kvara vertico tiam okazas en eno de la triangulo kaj informo pri ĝia situo estas tiam perdita.

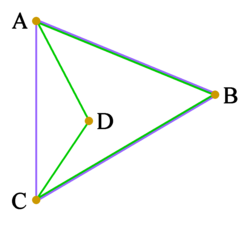
ABCD estas nekonveksa kvarlatero (verda). Ĝia situo de verticoj estas aro {A, B, C, D}. Ĝia konveksa koverto estas triangulo ABC (blua). Situo de verticoj de la konveksa koverto estas aro {A, B, C}, kiu estas malsama de situo de verticoj de la fonta kvarlatero. Do en ĉi tiu okazo, konveksa koverto ne estas taŭga maniero por priskribi situon de verticoj.

Ankaŭ malfiniaj kahelaroj povas komunigi situon de verticoj.

Triangula kahelaro	Romba kahelaro
Du malsamaj kahelaroj kun la sama situo de verticoj