
Back Gran dirombidodecàedre dixato Catalan Great disnub dirhombidodecahedron English Granda duriproĉa durombo-dekduedro Esperanto Grand dirhombidodécaèdre disadouci French 大二重変形二重斜方十二面体 Japanese Marele dirombidodecaedru disnub Romanian Veliki dvojno prirezan dirombidodekaeder Slovenian 大二重扭稜二重斜方十二面體 Chinese
| Gran dirrombidodecaedro birromo | ||
|---|---|---|
| Familia: Poliedros uniformes estrellados | ||
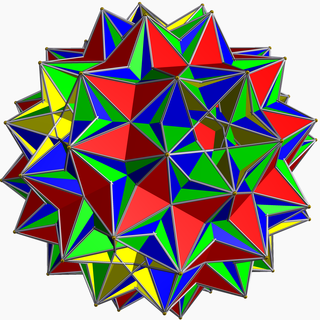 Imagen del sólido | ||
| Caras | 204 | |
| Polígonos que forman las caras |
120 triángulos equiláteros 60 cuadrados 24 pentagramas | |
| Aristas | 360 | |
| Vértices | 60 | |
| Configuración de vértices |
 (5⁄2.4.3.3.3.4.5⁄3.4.3⁄2.3⁄2.3⁄2.4)/2 | |
| Grupo de simetría | Ih, [5,3], *532 | |
| Poliedro dual | Gran dirrombidodecacrono birromo | |
| Propiedades | ||
|
Poliedro no convexo de vértices uniformes Hemipoliedro | ||

En la geometría, el gran dirrombidodecaedro birromo, también llamado la figura de Skilling, es un poliedro estrellado uniforme degenerado.
Se demostró en 1970 que solo hay 75 poliedros uniformes además de las familias infinitas de prismas y antiprismas.[1] John Skilling descubrió otro ejemplo degenerado, el dirrombidodecaedro birromo, al relajar la condición de que las aristas deben no sobrelaparse. De manera más precisa, permitió que cualquier cantidad par de caras se interesacaran en una sola arista, siempre y cuando la figura no pudiera ser separada en dos conjuntos de caras conectados.[2] Debido a que su realización geométrica tiene algunas aristas dobles en las cuales cuatro caras se encuentran, se considera un poliedro uniforme degenerado pero no estrictamente un poliedro uniforme.
El número de aristas es ambiguo, pues el poliedro abstracto subyacente tiene 360 aristas, pero 120 pares de estas tienen la misma imagen en la realización geométrica, por lo que la realización geométrica tiene 120 aristas simples y 120 aristas dobles, para un total de 240 aristas. La característica de Euler del poliedro abstracto es −96. Si las parejas de aristas coincidentes en la realización geométrica se consideran una sola arista, entonces el poliedro solo tiene 240 aristas y característica de Euler 24.
La figura del vértice tiene 4 caras cuadradas que pasan por el centro del modelo.
Se puede construir como la disyunción exclusiva del gran dirrombicosidodecaedro y el compuesto de veinte octaedros.
- ↑ Sopov, S. P. (1970). «A proof of the completeness on the list of elementary homogeneous polyhedra». Ukrainskiui Geometricheskiui Sbornik (en ruso) (8): 139-156.
- ↑ Skilling, J. (1975). «The Complete Set of Uniform Polyhedra». Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 278 (1278): 111-112. doi:10.1098/rsta.1975.0022.