
Back مبرهنة فيفياني Arabic Теорема на Вивиани Bulgarian Teorema de Viviani Catalan Satz von Viviani German Θεώρημα Βιβιάνι Greek Viviani's theorem English Viviani-ren teorema Basque Vivianin lause Finnish Théorème de Viviani French משפט ויויאני HE
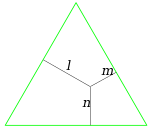
El teorema de Viviani, llamado así en honor del matemático florentino Vincenzo Viviani, enuncia que en un triángulo equilátero la suma de las distancias desde un punto interior de él a cada uno de los lados es igual a la altura del triángulo. Viviani demostró un resultado más general en su libro De Maximis et Minimis Geometrica Divinatio in Quintum Conicorum Apollonii Pergaei, de 1659.
El teorema se puede extender a polígonos equiláteros y polígonos equiangulares. Específicamente, la suma de las distancias desde un punto hasta los lados de un polígono equilátero o equiangular no depende del punto.[1]
- ↑ Elias Abboud "On Viviani’s Theorem and its Extensions" pp. 2, 11 (en inglés)