Collatzen aierua

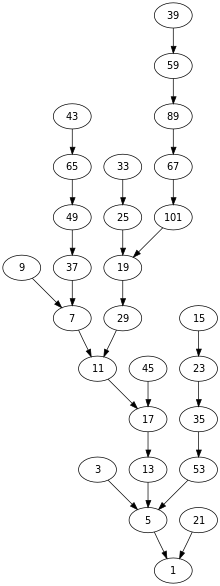
Collatzen aierua matematikako aieru bat da, honela definitutako sekuentziei dagokiena: hasi edozein zenbaki oso positiborekin n. Beraz, termino bakoitza honela ateratzen da aurreko terminotik: aurreko terminoa bikoitia bada, hurrengo terminoa aurreko terminoaren erdia da. Aurreko terminoa bakoitia bada, hurrengo terminoa aurreko terminoa bider 3 gehi 1 da. Ustea zera da, n-ren balioa zeinahi dela ere, sekuentzia beti iritsiko da 1 zenbakira.

Lothar Collatz matematikariarengandik hartu du izena aieruak, 1937an sartu baitzuen ideia, doktoretza jaso eta bi urtera. Izen hauek ere hartzen ditu aieruak: 3n + 1 arazoa, 3n + 1 aierua, Ulamen aierua (Stanisاaw Ulamen arabera), Kakutaniren arazoa (Shizuo Kakutaniren arabera), Thwaitesen aierua (Sir Bryan Thwaitesen arabera), Hasseren algoritmoa (Helmut Hasseren arabera), edo Sirakusako arazoa.^[1] Parte hartzen duten zenbakien sekuentziari, batzuetan, kazkabar-sekuentzia edo txingor-zenbakiak esaten zaio (izan ere, balioek, oro har, jaitsiera eta igoera ugari izaten dituzte, hala nola hodei bateko txingorra), edo zenbaki zoragarriak.

1. ↑ «3n+1: iturri txiki baten emari handia» Zientzia Kaiera 2020-03-18 (Noiz kontsultatua: 2021-10-25).