Pascalin simpukka

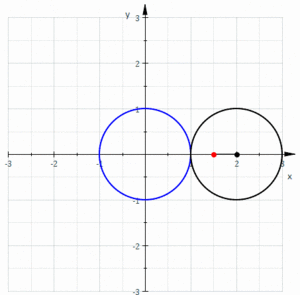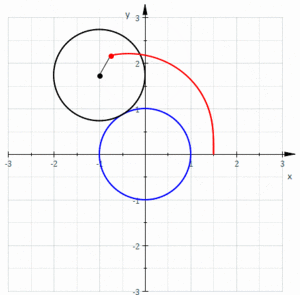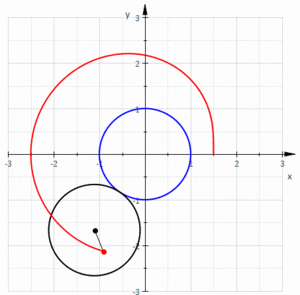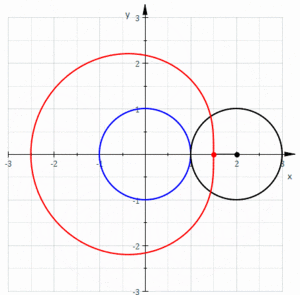
Pascalin simpukka^[1] (ransk. limaçon de Pascal) on geometriassa vierintäkäyrä, jonka muodostaa ympyrään sidotun pisteen liikerata, kun tämä ympyrä vierii ulkopuolitse toisen samansäteisen ympyrän ympäri. Se voidaan yhtäpitävästi määritellä myös ympyrään sidotun pisteen liikeradaksi, kun suurempi ympyrä vierii pienemmän ympyrän ympäri, jonka säde on puolet suuremman ympyrän säteestä ja tämä pienempi ympyrä on suuremman ympyrän sisällä. Näin ollen Pascalin silmukka kuuluu keskipisteellisten trokoidien, tarkemmin sanottuna epitrokoidien^[2] ryhmään.

Nimitys limaçon johtuu ranskan kielen sanasta limaçon, joka tarkoittaa etanaa (lat. limax).^[3] Riippuen siitä, missä kohdassa käyrän generoiva piste sijaitsee, sillä voi olla sisä- tai ulkopuolisia silmukoita, mihin sen nimikin viittaa, mutta se voi olla myös sydämen muotoinen tai soikea kupera käyrä. Kardioidi on Pascalin simpukan erikoistapaus, jossa liikkuva piste on pyörivällä ympyrällä. Se on sydämen muotoinen, ja sillä on sisään työntyvä kärkipiste.

Pascalin silmukka on neljännen asteen käyrä.^[2]

1. ↑ David Bergamini: ”Käyrien ja lukujen onnistunut liitto”, Lukujen maailma, s. 84. (lähde suomenkieliselle nimelle) Suomentanut Pertti Jotuni. Sanoma Osakeyhtiö, 1972.
2. ↑ ^{a b} limaçon 2dcurves.com. Viitattu 6.9.2017.
3. ↑ Howard Anton: ”Families of cardioids and limaçon”, Calculus, s. 725. Wiley & Sons, 1984. Teoksen verkkoversio.