Cube adouci

Cube adouci

Éléments

Faces	Arêtes	Sommets
38 triangles et carrés	60	24 de degré 5

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	Semi-régulier et convexe, chiral
Volume (arête a)	${\displaystyle {\frac {{\sqrt {2\tau }}(7\tau ^{2}+1)}{6}}a^{3}}$ où ${\displaystyle \tau }$ est la constante de Tribonacci
Aire de surface	${\displaystyle (6+8{\sqrt {3}})a^{2}}$
Groupe de symétrie	O
Dual	Icositétraèdre pentagonal

modifier

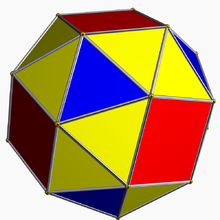
Le cube adouci, ou cube camus^[1], ou encore snub cube est un solide d'Archimède.

Le cube adouci possède 38 faces dont 6 sont des carrés et les 32 autres sont des triangles équilatéraux. Il possède 60 arêtes et 24 sommets. Il a deux formes distinctes, qui sont leurs images dans un miroir (ou "énantiomorphes") l'un de l'autre.

Étant obtenu par adoucissement (en) du cube et de l'octaèdre, il est aussi appelé cuboctaèdre adouci.