Nombre pratique

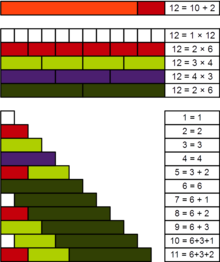
En arithmétique, un entier strictement positif n est dit pratique ou panarithmique si tout entier compris entre 1 et n est somme de certains diviseurs (distincts) de n.

Par exemple, 8 est pratique. En effet, il a pour diviseurs 1, 2, 4 et 8, or 3 = 2 + 1, 5 = 4 + 1, 6 = 4 + 2 et 7 = 4 + 2 + 1.

Les douze premiers nombres pratiques sont 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28 et 30 (suite A005153 de l'OEIS).

Les nombres pratiques ont été utilisés par Fibonacci pour représenter des nombres rationnels par des fractions égyptiennes. Fibonacci ne définit pas formellement les nombres pratiques mais donne une table de développements en fractions égyptiennes pour des fractions dont le dénominateur est pratique.

Les nombres pratiques ont été baptisés ainsi en 1948 par Srinivasan^[1] ; il commença à les classifier, ce qui fut achevé par Stewart et Sierpiński. Cette caractérisation permet de déterminer si un nombre est pratique à partir de sa décomposition en facteurs premiers et de montrer que d'autres ensembles remarquables d'entiers ne contiennent que des nombres pratiques.

Les nombres pratiques sont analogues aux nombres premiers par beaucoup de leurs propriétés.