
Back إسقاط مركزي Arabic Zentralprojektion German Proyección central Spanish Centrális projekció Hungarian 透视投影 Chinese
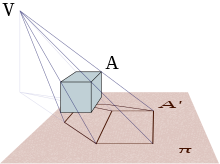

En géométrie de l'espace, une projection centrale, ou projection conique, ou encore perspective centrale, est définie de la manière suivante. Soit V un point , appelé centre ou sommet de la projection et un plan ne contenant pas V, on appelle projection centrale sur de sommet V, la fonction qui, à tout point A distinct de V, associe le point d'intersection A', s'il existe, de la droite (VA) avec le plan .
Par exemple, les ombres portées sur une surface plane par une source de lumière ponctuelle est une projection conique
L'étude des projections centrales s'est développée principalement à partir du XVe siècle pour les dessins en perspective linéaire avant d'avoir son développement propre, à partir de 1636, avec les travaux de Girard Desargues, puis ceux de Gaspard Monge et de Jean-Victor Poncelet. Elle a donné naissance à une nouvelle géométrie appelée la géométrie projective.

