Back شبيه متجه Arabic Pseudovector Catalan Псевдовектор CV Pseudovektor German Pseudovector English Vector axial Spanish شبهبردار Persian Pseudovektori Finnish Pseudovettore Italian 擬ベクトル Japanese
En physique, un pseudovecteur ou vecteur axial est un vecteur de dimension 3 dont le sens dépend de l'orientation de l'espace. Plus précisément, l'inversion de l'orientation de l'espace se traduit par un changement de sens du pseudovecteur qui est donc changé en son opposé. On parle de pseudovecteurs par opposition aux vecteurs « ordinaires » (dits polaires) qui sont invariants par une telle inversion. Le produit vectoriel de deux vecteurs polaires est l'exemple type du pseudovecteur.
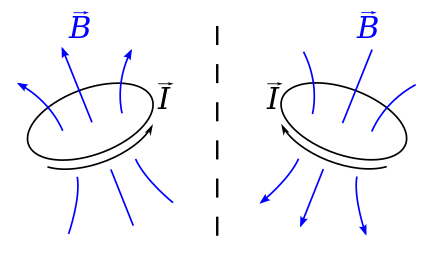
Pour satisfaire aux lois de la physique, on transforme un vecteur axial de la même manière qu'un vecteur polaire lors d'une isométrie directe (conservant les angles orientés comme une rotation) mais différemment lors d'une isométrie indirecte, par exemple une symétrie par rapport à un point ou par rapport à un plan[1] (voir la figure ci-dessous).
Les règles de calcul concernant les vecteurs axiaux sont ainsi différentes de celles des vecteurs polaires. Elles sont liées à celles des pseudo-vecteurs mathématiques (c'est-à-dire des bivecteurs), par exemple une 2-forme différentielle. En effet, une forme différentielle de degré 2 peut être représentée par une matrice antisymétrique de trois lignes et trois colonnes, possédant donc seulement trois composantes indépendantes auxquelles on peut faire correspondre un vecteur appelé vecteur dual. Si on considère les vecteurs duaux du bivecteur et de son transformé, ils se correspondent selon la loi des vecteurs axiaux (voir la figure ci-dessous et ici) et non selon la loi des vecteurs polaires[2].