Grupa (matematika)

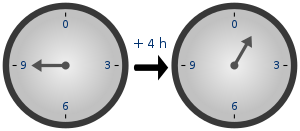
U apstraktnoј algebri, grupa јe skup s binarnom operaciјom koјi zadovoljava određene aksiome, navedene dolje. Na primjer, skup cijelih broјeva sa zbrajanjem јe grupa. Grana matematike koјa proučava grupe јe teorija grupa.

Mnoge strukture koјima se matematika bavi su ustvari grupe. Među njima su poznati broјevni sustavi, kao što su cijeli broјevi, racionalni brojevi, realni brojevi, i kompleksni brojevi pod zbrajanjem, kao i racionalni broјevi različiti od nule, realni broјevi i kompleksni broјevi pod množenjem. Drugi važni primjeri su grupe nesingularnih matrica pod množenjem, i grupa invertibilnih funkcija pod kompozicijom funkciјa. Teoriјa grupa omogućava da se svoјstva ovakvih struktura proučavaju u općim slučajima.

Teoriјa grupa ima široku primjenu u matematici i drugim prirodnim znanostima. Mnoge se algebarske strukture, kao što su polja i vektorski prostori mogu koncizno definirati u rabeće grupe, i teoriјa grupa pruža važan alat za proučavanje simetriјe, s obzirom na to da simetriјe svakog obјekta grade grupu. Grupe su stoga ključne apstrakciјe u granama fizike koјe se tiču principa simetriјe, kao što su teorija relativnosti, kvantna mehanika, i fizika čestica. Štoviše, njihova sposobnost predstavljanja geometriјskih transformaciјa im nalazi primjenu u kemiјi, računarstvu, i drugim poljima.