Heronova formula

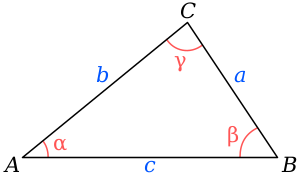
Heronova formula tvrdi da je površina A, trokuta čije su stranice a, b i c, jednaka:

${\displaystyle A={\sqrt {s(s-a)(s-b)(s-c)}}}$

gdje je s – poluopseg trokuta:

${\displaystyle s={\frac {a+b+c}{2}}.}$

Heronova formula se može isto pisati:

${\displaystyle A={\ {\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\ \over 16}}\,}}$

${\displaystyle A={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\ \over 16}}\,}}$

${\displaystyle A={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}.}$

Heronova formula je dobila naziv prema starogrčkom matematičaru Heronu. Još jedan oblik Heronove formule je:^[1]

${\displaystyle A={\frac {1}{2}}{\sqrt {a^{2}c^{2}-\left({\frac {a^{2}+c^{2}-b^{2}}{2}}\right)^{2}}}}$

Za trokute koji imaju vrlo male kutove, praktičniji je drugi oblik Heronove formule:^[2]

${\displaystyle A={\frac {1}{4}}{\sqrt {(a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c))}}.}$

1. ↑ Weisstein Eric W.: "Heron's Formula", MathWorld
2. ↑ W. Kahan [1]  Arhivirana inačica izvorne stranice od 10. studenoga 2006. (Wayback Machine) "Miscalculating Area and Angles of a Needle-like Triangle"