Titik kritis (matematika)

Artikel ini sudah memiliki referensi, tetapi tidak disertai kutipan yang cukup. Anda dapat membantu mengembangkan artikel ini dengan menambahkan lebih banyak kutipan pada teks artikel. (Januari 2015) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini)

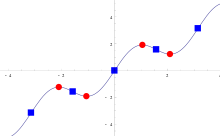
Titik kritis adalah istilah umum yang digunakan dalam banyak cabang matematika.

Ketika berhadapan dengan fungsi dari variabel real, titik kritis adalah titik dalam domain fungsi di mana fungsi tersebut tidak dapat didiferensialkan atau nilai turunannya sama dengan nol.^[1] Ketika berurusan dengan variabel kompleks, titik kritis adalah, sama halnya, titik dalam domain fungsi yang mengakibatkan fungsi tersebut tidak holomorfik atau turunannya sama dengan nol.^[2][3] Demikian juga, untuk fungsi dari beberapa variabel real, titik kritis adalah nilai dalam domainnya sehingga gradiennya tidak terdefinisi atau sama dengan nol.^[4]

Nilai fungsi pada titik kritis disebut dengan nilai kritis.

Definisi semacam ini dapat diperumum ke peta terdiferensialkan antara ${\displaystyle \mathbb {R} ^{m}}$ dan ${\displaystyle \mathbb {R} ^{n}}$. Sebuah titik kritis, dalam hal ini, adalah sebuah titik yang mengakibatkan rank dari matriks Jacobi tidak maksimum. Definisi ini juga dapat diperumum lebih jauh ke peta terdiferensialkan antara lipatan-lipatan terdiferensialkan, sebagai titik-titik yang mengakibatkan rank dari matriks Jacobi berkurang. Dalam hal ini, titik-titik kritis juga disebut titik bifurkasi.

1. ^ Problems in mathematical analysis. Demidovǐc, Boris P., Baranenkov, G. Moscow(IS): Moskva. 1964. ISBN 0846407612. OCLC 799468131. 
2. ^ Stewart, James (2008). Calculus : early transcendentals (edisi ke-6th). Belmont, CA: Thomson Brooks/Cole. ISBN 9780495011668. OCLC 144526840. 
3. ^ Larson, Ron (2010). Calculus. Edwards, Bruce H., 1946- (edisi ke-9th). Belmont, Calif.: Brooks/Cole, Cengage Learning. ISBN 9780547167022. OCLC 319729593. 
4. ^ Adams, Robert A.; Essex, Christopher (2009). Calculus: A Complete Course. Pearson Prentice Hall. hlm. 744. ISBN 978-0-321-54928-0.