Numero armonico

In matematica, per ogni intero naturale n si definisce come n-esimo numero armonico la somma:

${\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}}$

Si tratta evidentemente di numeri razionali e si dimostra che le corrispondenti frazioni ridotte ai minimi termini hanno numeratore dispari e denominatore pari.

In concreto i primi termini della successione dei numeri armonici sono:

1, 3/2, 11/6, 25/12, 137/60, 49/20, 363/140, 761/280, 7129/2520, 7381/2520, 83711/27720, ...

I numeratori dei numeri armonici sono detti numeri di Wostenholme e costituiscono la successione A001008 dell'OEIS. I denominatori costituiscono la successione A002805 dell'OEIS.

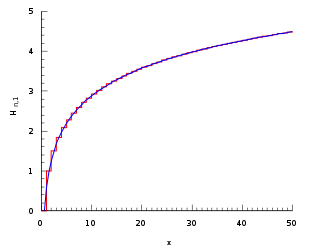
I numeri armonici costituiscono le somme parziali della serie armonica, notoriamente divergente.