
Back Vektorruimte Afrikaans فضاء متجهي Arabic Espaciu vectorial AST Векторлы арауыҡ Bashkir Вектарная прастора Byelorussian Линейно пространство Bulgarian वेक्टर स्पेस Bihari সদিক রাশির বীজগণিত Bengali/Bangla Vektorski prostor BS Espai vectorial Catalan
Een vectorruimte, ook lineaire ruimte genoemd, is een wiskundige structuur die wordt gevormd door een verzameling elementen die vectoren worden genoemd, die bij elkaar kunnen worden opgeteld en die kunnen worden vermenigvuldigd met getallen die in deze context scalairen worden genoemd. Vaak zijn de scalairen reële getallen, maar er bestaan ook vectorruimten waarin de scalairen complexe getallen, rationale getallen of heel algemeen elementen van een willekeurig veld (Vlaams) of lichaam (Nederlands) zijn. Dat hangt van de definitie af. De operaties van vectoroptelling en scalaire vermenigvuldiging moeten aan bepaalde eisen voldoen, de zogenaamde axioma's.
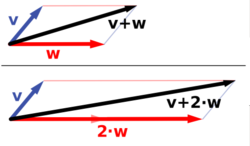
De euclidische vectorruimte is voor elke dimensie een voorbeeld van een vectorruimte. De twee- en driedimensionale euclidische vectorruimte worden vaak gebruikt om natuurkundige grootheden, zoals krachten weer te geven: elke twee krachten (van hetzelfde type) kunnen worden opgeteld met als resultaat een derde kracht, de resultante, en de scalaire vermenigvuldiging van een krachtvector met een reële factor is opnieuw een krachtvector. Als meer meetkundig voorbeeld, vormen vectoren die translaties in het vlak of in de driedimensionale ruimte weergeven, ook vectorruimten.
Vectorruimten vormen een belangrijk onderwerp van studie binnen de lineaire algebra. De theorie wordt verder verrijkt door aan een vectorruimte extra structuur, zoals een norm of een inwendig product, toe te kennen. Zulke vectorruimten komen van nature voor in de wiskundige analyse, vooral in de gedaante van oneindig-dimensionale functieruimten waarvan de vectoren functies zijn. Een belangrijke vraag is of een rij vectoren naar een bepaalde vector convergeert. Het antwoord op deze vraag kan worden gegeven door vectorruimten met aanvullende gegevens te bestuderen, meestal vectorruimten die zijn uitgerust met een gepaste topologie, die het mogelijk maakt om begrippen als afstand en continuïteit in beschouwing te nemen. Dit soort verrijkte topologische vectorruimten, met name banachruimten en hilbertruimten, hebben een rijkere theorie.
Historisch gesproken kunnen de eerste ideeën die hebben geleid tot vectorruimten, teruggevoerd worden tot de 17e-eeuwse analytische meetkunde, matrices, stelsels lineaire vergelijkingen en euclidische vectoren. De moderne, meer abstracte behandeling werd in de late 19e eeuw voor het eerst door Giuseppe Peano geformuleerd en omvat meer algemene objecten dan de euclidische ruimte. Veel van de theorie kan worden gezien als een uitbreiding van de klassieke meetkundige ideeën, zoals lijnen, vlakken en hun hogerdimensionale generalisaties.
Vectorruimten vindt men in de gehele wiskunde, de natuurwetenschappen en de technische wetenschappen. Zij vormen het geschikte algebraïsche begrip om met stelsels lineaire vergelijkingen om te gaan. Ook bieden zij een raamwerk voor de fourierreeksen, die worden gebruikt in algoritmen voor beeldcompressie, en bieden zij een omgeving die kan worden gebruikt voor oplossingstechnieken voor partiële differentiaalvergelijkingen. Bovendien leveren vectorruimten een abstracte manier van omgaan met meetkundige en natuurkundige objecten, zoals tensoren, die op hun beurt het onderzoek van de lokale eigenschappen van variëteiten door linearisatietechnieken mogelijk maken. Het begrip vectorruimte kan ook in verschillende richtingen worden gegeneraliseerd, wat tot geavanceerde begrippen leidt in de meetkunde en de abstracte algebra.
| Algebraïsche structuur | ||
|---|---|---|
|
Groep · Halfgroep · Ideaal · Lichaam/veld · Magma · Monoïde · Ring |