Ekstremum funkcji

Ten artykuł od 2022-01 wymaga zweryfikowania podanych informacji.

Należy podać wiarygodne źródła w formie przypisów bibliograficznych.
Część lub nawet wszystkie informacje w artykule mogą być nieprawdziwe. Jako pozbawione źródeł mogą zostać zakwestionowane i usunięte.
Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary)
Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu.
Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

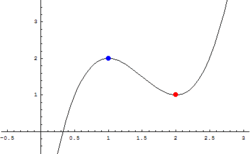
Ekstremum funkcji (l. mn. ekstrema; z łac. extrēmus – najdalszy, ostatni) – maksymalna lub minimalna wartość funkcji^[1].

• Funkcja ${\displaystyle f(x)}$ przyjmuje w punkcie ${\displaystyle x_{0}}$ maksimum lokalne (odpowiednio: minimum lokalne), jeśli w pewnym otwartym^[a] otoczeniu tego punktu (np. w pewnym przedziale otwartym) funkcja nigdzie nie ma wartości większych (odpowiednio: mniejszych).
• Jeśli dodatkowo w pewnym otwartym sąsiedztwie punktu ${\displaystyle x_{0}}$ funkcja nie ma również wartości równych ${\displaystyle f(x_{0}),}$ to jest to maksimum (odpowiednio: minimum) lokalne właściwe.
• Minima i maksima lokalne są zbiorczo nazywane ekstremami lokalnymi.
• Największa i najmniejsza wartość funkcji w całej dziedzinie nazywane są odpowiednio maksimum i minimum globalnym, a zbiorczo ekstremami globalnymi.

Obrazowo: Na powierzchni Ziemi maksimum globalne wysokości nad poziomem morza występuje na szczycie Mount Everestu, maksimum lokalnym jest szczyt każdego pagórka. Jeśli szczyt pagórka jest poziomy i płaski (a także niekiedy w innych przypadkach^[b]), nie będzie to maksimum lokalne właściwe.

Istnieją funkcje nieposiadające ekstremów lokalnych ani globalnych, np. funkcja ${\displaystyle f(x)=x.}$

Poszukiwanie ekstremów jest ważne w praktycznych zastosowaniach matematyki, na przykład w technice i statystyce. Wiele zagadnień optymalizacyjnych sprowadza się do poszukiwania ekstremów odpowiednich funkcji, jak na przykład funkcji kosztu, albo miary jakości dla różnych parametrów danego urządzenia.

Teoria ekstremów w naturalny sposób ma silny związek z teorią nierówności: wiele problemów i twierdzeń można formułować równoważnie zarówno w języku ekstremów, jak i nierówności, co rzuca światło na obie te dziedziny.