Escada de Penrose

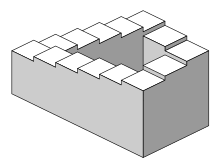
A escada de Penrose ou os degraus de Penrose, também apelidada de escada impossível, é um objeto impossível criado por Oscar Reutersvärd em 1937^[1][2][3][4] e posteriormente tornado, independentemente, popular por Lionel Penrose e seu filho Roger Penrose.^[5] Ela é, uma variação do triângulo de Penrose, uma representação bidimensional de uma escada em que as escadas fazem quatro curvas de 90 graus conforme sobem ou descem, mas formam um loop contínuo, de modo que uma pessoa pode escalá-las para sempre e nunca mais alto. Isso é claramente impossível na geometria euclidiana tridimensional.

A "escada contínua" foi apresentada pela primeira vez em um artigo que os Penroses escreveram em 1959, baseado no chamado "triângulo de Penrose" publicado por Roger Penrose no jornal britânico de psicologia (em 1958).^[5] M.C. Escher então descobriu as escadarias de Penrose no ano seguinte e fez sua, agora famosa, litografia Klimmen en dalen (Subindo e Descendo) em março de 1960. Penrose e Escher foram informados sobre o trabalho um do outro naquele mesmo ano.^[6] Escher aprofundou o tema em sua impressão Waterval (Cachoeira), publicada em 1961.

Em seu artigo original, os Penroses observaram que "cada parte da estrutura é aceitável, como representando um lance de degraus, mas as conexões são tais que a imagem, como um todo, é inconsistente: os degraus descem continuamente no sentido horário."^[7]