Problema de Monty Hall

Este artigo ou secção contém uma lista de referências no fim do texto, mas as suas fontes não são claras porque não são citadas no corpo do artigo, o que compromete a confiabilidade das informações. Ajude a melhorar este artigo inserindo citações no corpo do artigo. (Fevereiro de 2014)

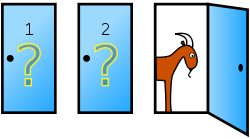
O problema de Monty Hall, também conhecido por paradoxo de Monty Hall, é um problema matemático e paradoxo que surgiu a partir de um concurso televisivo dos Estados Unidos chamado Let’s Make a Deal, exibido na década de 1970.

O jogo consistia no seguinte: Monty Hall, o apresentador, apresentava três portas aos concorrentes. Atrás de uma delas estava um prêmio (um carro) e, atrás das outras duas, dois bodes.

1. Na 1.ª etapa o concorrente escolhe uma das três portas (que ainda não é aberta);
2. Na 2.ª etapa, Monty abre uma das outras duas portas que o concorrente não escolheu, revelando que o carro não se encontra nessa porta e revelando um dos bodes;
3. Na 3.ª etapa Monty pergunta ao concorrente se quer decidir permanecer com a porta que escolheu no início do jogo ou se ele pretende mudar para a outra porta que ainda está fechada para então a abrir. Agora, com duas portas apenas para escolher — pois uma delas já se viu, na 2.ª etapa, que não tinha o prêmio — e sabendo que o carro está atrás de uma das restantes duas, o concorrente tem que tomar a decisão.

Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Por quê?

Na realidade não é assim tão indiferente mudar ou ficar com a primeira escolha. No início, quando se escolheu uma das portas, havia 1/3 de probabilidade de ganhar o carro. Não existe razão aparente para essa probabilidade mudar após Monty Hall ter aberto uma das portas que não era premiada. As outras duas portas não escolhidas tinham em conjunto 2/3 de probabilidade de ocultarem o carro, e quando uma dessas portas é aberta (por não ter prêmio) a porta não escolhida que continua fechada passa a ter 2/3 de probabilidade de ser a porta do carro.

A confusão é feita seguindo o raciocínio que parece mais lógico: "mas a porta escolhida também continua fechada... então cada uma das portas fechadas passa a ter 1/2 de chance de ter o carro?".