Prime number

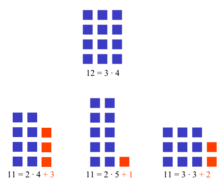
A prime number is a natural number that has exactly two divisors: one and itself. A natural number can be gotten by multiplying two numbers. These two numbers are called its divisors. Any natural number is equal to one times the number itself, so those two numbers are two of its divisors. A prime number is a number with only two divisors: one and itself.^[1]

The prime numbers are the numbers other than one which are not equal to ${\displaystyle m\times n}$ (except one times itself). The smallest prime number is two. The next prime numbers are 3, 5, 7, 11, and 13. The set of prime numbers is sometimes written as ${\displaystyle \mathbb {P} }$.^[2]

If the number has any other divisors besides one and itself, then the number is called a composite number. The smallest composite number is four, because two times two equals four; thus four has three divisors. One is not a composite number, but it is also not a prime number because it only has one divisor which is one.^[1]

The fundamental theorem of arithmetic states that every positive integer can be written as a product of primes in a unique way,^[3] though the way the prime numbers occur is a difficult problem for mathematicians. When a number is larger, it is more difficult to know if it is a prime number. One of the answers is the prime number theorem. One of the unsolved problems is Goldbach's conjecture.

There is no largest prime number. One of the most famous mathematicians, Euclid, recorded a proof that there is no largest prime number. However many scientists and mathematicians are still searching to find it as part of the Great Internet Mersenne Prime Search.

1. ↑ ^{1.0 1.1} C, Mohamed. "Is 1 a prime number or not?". www.tutorocean.com. Retrieved 2021-10-04.
2. ↑ "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-10-07.
3. ↑ Weisstein, Eric W. "Prime Number". mathworld.wolfram.com. Retrieved 2020-10-07.