Standard deviation

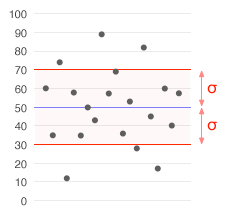
Standard deviation is a number used to tell how measurements for a group are spread out from the average (mean or expected value).^[1] A low standard deviation means that most of the numbers are close to the average, while a high standard deviation means that the numbers are more spread out.^[2][3]

The reported margin of error is usually twice the standard deviation. Scientists commonly report the standard deviation of numbers from the average number in experiments. They often decide that only differences bigger than two or three times the standard deviation are important. Standard deviation is also useful in money, where the standard deviation on interest earned shows how different one person’s interest earned might be from the average.

Many times, only a sample, or part of a group can be measured. Then a number close to the standard deviation for the whole group can be found by a slightly different equation called the sample standard deviation, explained below. In which case, the standard deviation of the whole group is represented by the Greek letter ${\displaystyle \sigma }$, and that of the sample by ${\displaystyle s}$.^[4]

1. ↑ "What is the Standard Deviation? | Data Basecamp". 2023-03-22. Retrieved 2023-05-29.
2. ↑ Gauss, Carl Friedrich (1816). "Bestimmung der Genauigkeit der Beobachtungen". Zeitschrift für Astronomie und verwandt Wissenschaften. 1: 187–197.
3. ↑ Walker, Helen (1931). Studies in the History of the Statistical Method. Baltimore, MD: Williams & Wilkins Co. pp. 24–25.
4. ↑ "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-08-21.