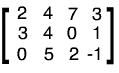Linearna algebra

Nekateri predmeti, ki jih proučuje linearna algebra Vektor V tridimenzionalnem evklidskem prostoru te tri ravnine predstavljajo rešitve linearnih enačb, njihov presek pa skupek skupnih rešitev: v tem primeru ena točka. Modra črta je skupna rešitev dveh enačb. Linearne transformacije Sistemi linearnih enačb Matrike ${\displaystyle \mathbf {A} {\color {Red}\xi }={\color {Blue}\lambda }{\color {Red}\xi }}$ Lastne vrednosti in lastni vektorji Kvadriki Tenzorji

Linearna algebra je matematična disciplina, ki se ukvarja s proučevanjem vektorjev, vektorskih prostorov (ali linearnih prostorov), linearnih transformacij in sistemov linearnih enačb. Konkretno upodobitev linearne algebre najdemo v analitični geometriji. Vektorski prostori so osrednja tema sodobne matematike; torej se linearna algebra na široko uporablja v abstraktni algebri in funkcionalni analizi. Zelo je uporabna tudi v naravoslovnih in družboslovnih znanostih.

Nanaša na linearne enačbe, kot so:

${\displaystyle a_{1}x_{1}+\cdots +a_{n}x_{n}=b,}$

linearne transformacije, kot so:

${\displaystyle (x_{1},\ldots ,x_{n})\mapsto a_{1}x_{1}+\cdots +a_{n}x_{n},}$

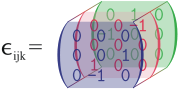
in njihove predstavitve v vektorskih prostorih in skozi matrice.^[1][2][3]

Linearna algebra je osnova za skoraj vsa področja matematike. Na primer, linearna algebra je temeljna v sodobnih predstavitvah geometrije, vključno z definicijami osnovnih objektov, kot so črte, ravnine in rotacije. Tudi funkcionalno analizo, vejo matematične analize, lahko razumemo kot aplikacijo linearne algebre v prostorih funkcij.

Linearna algebra se uporablja tudi v velikem številu znanostih in področij tehnike, saj omogoča modeliranje številnih naravnih pojavov in učinkovito računanje s takšnimi modeli. Za nelinearne sisteme, ki jih ni mogoče modelirati z linearno algebro, se pogosto uporabljajo približki prvega reda.

1. ↑ Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1. izd.), Chapman and Hall/CRC, ISBN 978-1420095388
2. ↑ Strang, Gilbert (19. julij 2005), Linear Algebra and Its Applications (4th izd.), Brooks Cole, ISBN 978-0-03-010567-8
3. ↑ Weisstein, Eric. »Linear Algebra«. From MathWorld--A Wolfram Web Resource. Wolfram. Pridobljeno 16. aprila 2012.