Gyllene snittet

För andra betydelser, se Gyllene snittet (olika betydelser).

Gyllene snittet (φ)
Irrationella tal  ζ(3) – E – e – γ – δ – φ – √2 – √3 – √5 – π – ρ – ρ – δS – 12√2
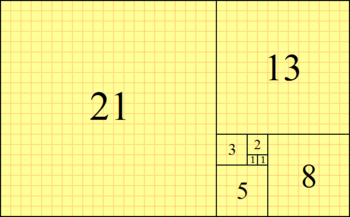Fibonaccitalen approximerar den gyllene rektangeln, som har sidlängderna 1 och gyllene snittet
Decimalutveckling	1,61803 39887 49894 84820 45868 ...

Gyllene snittet, på latin: sectio aurea, är det förhållande som erhålls när en sträcka delas i en längre del a och en kortare del b så att hela sträckan a + b förhåller sig till a som a förhåller sig till b^[1]:

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}}$

Gyllene snittet brukar betecknas med φ (den grekiska bokstaven fi). Det gyllene snittets värde är

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1,618033988749}$

Ofta används också det omvända förhållandet 1/φ. Detta värde brukar betecknas med Φ (ett versalt fi):

${\displaystyle \Phi ={\frac {b}{a}}\approx 0,618033988749}$

En rektangel vars sidor förhåller sig som det gyllene snittet kallas den gyllene rektangeln.

Gyllene snittet var känt redan av Pythagoras och de gamla grekerna och genom tiderna, kanske framför allt under renässansen, har man i detta förhållande velat se en norm för den fullkomliga harmonin hos mått och proportioner inom måleriet, fotokonsten, arkitekturen och bildhuggarkonsten.

Förespråkare har också velat se gyllene snittets proportioner i ett stort antal av naturens skapelser, något som dock har ifrågasatts.

Matematikerna i det antika Grekland intresserade sig för det man nu kallar gyllene snittet eftersom värdet ständigt dök upp i olika geometriska figurer och kroppar som pentagrammet och ikosaedern. Upptäckten av förhållandet brukar tillskrivas Pythagoras och hans följeslagare. Dessa hade en regelbunden femhörning, med ett inskrivet regelbundet pentagram, som symbol.

Den första exakta beskrivningen av gyllene snittet återfinns hos Euklides (cirka 300 f.Kr.). I sin Elementa betecknar han uppdelningen av en sträcka i gyllene snittets proportioner som "delning i extrem- och medelförhållande".^[2] Begreppet används i lösningen av flera av problemen i Elementa.^[3] Euklides beteckning var fram till mitten av 1800-talet den huvudsakligen använda.

Den medeltida matematikern och franciskanermunken Luca Pacioli (1445–1517) betecknar i sitt verk De Divina Proportione, publicerad i Venedig år 1509, det gyllene snittet som "det gudomliga förhållandet". I den andra delen av detta verk avhandlas den romerske arkitekten Vitruvius idéer om den mänskliga kroppens proportioner som utgångspunkt för arkitektur. Skriften innehåller illustrationer av Leonardo da Vinci som undervisades i matematik av Pacioli. I en annan av da Vincis berömda teckningar, den Vitruvianske mannen från runt 1492, kan man hitta ett approximativt gyllene snitt i förhållandet mellan kvadratens sida och cirkelns radie.

Namnet "det gyllene snittet" användes första gången 1835 av Martin Ohm, bror till Georg Ohm i en lärobok i matematik.^[4]