
Back Vergelyking (wiskunde) Afrikaans Gleichung ALS Ecuación AN समीकरण ANP معادلة رياضية Arabic معادلة رياضية ARZ সমীকৰণ Assamese Ecuación AST Tənlik Azerbaijani Тигеҙләмә Bashkir
You can help expand this article with text translated from the corresponding article in French. Click [show] for important translation instructions.
|
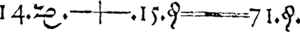
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =.[2][3] The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.[4]
Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables.[5][6]
The "=" symbol, which appears in every equation, was invented in 1557 by Robert Recorde, who considered that nothing could be more equal than parallel straight lines with the same length.[1]
- ^ a b Recorde, Robert, The Whetstone of Witte ... (London, England: Jhon Kyngstone, 1557), the third page of the chapter "The rule of equation, commonly called Algebers Rule."
- ^ "Equation - Math Open Reference". www.mathopenref.com. Retrieved 2020-09-01.
- ^ "Equations and Formulas". www.mathsisfun.com. Retrieved 2020-09-01.
- ^ Marcus, Solomon; Watt, Stephen M. "What is an Equation?". Retrieved 2019-02-27.
- ^ Lachaud, Gilles. "Équation, mathématique". Encyclopædia Universalis (in French).
- ^ "A statement of equality between two expressions. Equations are of two types, identities and conditional equations (or usually simply "equations")". « Equation », in Mathematics Dictionary, Glenn James et Robert C. James (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, p. 131.