Fiber diffraction is a subarea of scattering, an area in which molecular structure is determined from scattering data (usually of X-rays, electrons or neutrons). In fiber diffraction, the scattering pattern does not change, as the sample is rotated about a unique axis (the fiber axis). Such uniaxial symmetry is frequent with filaments or fibers consisting of biological or man-made macromolecules. In crystallography, fiber symmetry is an aggravation regarding the determination of crystal structure, because reflections are smeared and may overlap in the fiber diffraction pattern. Materials science considers fiber symmetry a simplification, because almost the complete obtainable structure information is in a single two-dimensional (2D) diffraction pattern exposed on photographic film or on a 2D detector. 2 instead of 3 co-ordinate directions suffice to describe fiber diffraction.
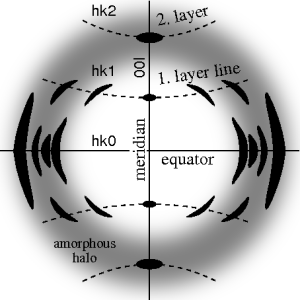
The ideal fiber pattern exhibits 4-quadrant symmetry. In the ideal pattern, the fiber axis is called the meridian, the perpendicular direction is called equator. In case of fiber symmetry, many more reflections than in single-crystal diffraction show up in the 2D pattern. In fiber patterns these reflections clearly appear arranged along lines (layer lines) running almost parallel to the equator. Thus, in fiber diffraction the layer line concept of crystallography becomes palpable. Bent layer lines indicate that the pattern must be straightened. Reflections are labelled by the Miller index hkl, i.e. 3 digits. Reflections on the i-th layer line share l=i. Reflections on the meridian are 00l-reflections. In crystallography artificial fiber diffraction patterns are generated by rotating a single crystal about an axis (rotating crystal method).
Non-ideal fiber patterns are obtained in experiments. They only show mirror symmetry about the meridian. The reason is that the fiber axis and the incident beam (X-rays, electrons, neutrons) cannot be perfectly oriented perpendicular to each other. The corresponding geometric distortion has been extensively studied by Michael Polanyi introducing the concept of Polanyi's sphere (German: "Lagenkugel") intersecting Ewald's sphere. Later Rosalind Franklin and Raymond Gosling have carried out their own geometrical reasoning and presented an approximative equation for the fiber tilt angle β. Analysis starts by mapping the distorted 2D pattern on the representative plane of the fiber. This is the plane that contains the cylinder axis in reciprocal space. In crystallography first an approximation of the mapping into reciprocal space is computed that is refined iteratively. The digital method frequently called Fraser correction starts from the Franklin approximation for the tilt angle β. It eliminates fiber tilt, unwarps the detector image, and corrects the scattering intensity. The correct equation for the determination of β has been presented by Norbert Stribeck.
